Vienas iš klausimų, į kurį reikia atsakyti norint pagaminti ventiliacijos groteles – koks turi būti kreipiančiųjų plokštelių skaičius. Šiame įraše pateikiama skaičiuoklė, kurios pagalba galima surasti optimalų plokštelių skaičių įvairaus aukščio grotelėms su įvairių matmenų plokštelėmis. Skaičiuoklėje optimaliu vadinamas toks grotelių plokštelių skaičius, kuriam esant grotelėmis galinčio judėti oro srautas yra didžiausias. Reiktų atkreipti dėmesį į tai, kad optimaliausias plokštelių skaičius ne visada bus „tinkamiausias”, pvz. optimaliu atveju gali būti, kad tarpas tarp dviejų plokštelių yra per didelis ir saugumo atžvilgiu jis nėra tinkamas. Dėl to, skaičiuoklės rezultatų lentelėje pateikiami visų galimų plokštelių skaičių duomenys, o optimaliausio plokštelių skaičiaus duomenys paryškinti žalia spalva.
Daugiau informacijos apie skaičiuoklę pateikiama žemiau.
Rezultatų lentelėje N žymi plokštelių skaičių, S – per groteles galinčio tekėti oro srauto ir grotelių priekinio paviršiaus plotų santykį, S0 – atstumą tarp dviejų plokštelių statmeniems plokštelių paviršiams kryptimi ir α – plokštelės pasukimo kampą.
Žemiau pateikiamas skaičiuoklėje naudojamas grotelių modelis ir skaičiuoklės veikimo principas.
Laikoma, kad grotelės yra stačiakampio formos, o kreipiančiosios plokštelės – stačiakampio gretasienio. Plokštelės išdėstytos horizontaliose padėtyse taip, kad vienos plokštelės išorinė briauna yra tokiame pačiame aukštyje kaip ir žemiau esančios plokštelės vidinė briauna, t. y. žiūrint į groteles statmena kryptimi vaizdo esančio už grotelių nesimato (žiūrėti brėžinį žemiau). Plokštelės viena kitos atžvilgiu išdėstytos lygiagrečiai. Taip pat neatsižvelgiama į jokius aerodinaminius reiškinius.

Per tokias groteles galinčio judėti oro srauto pločio santykis su grotelių priekinio paviršiaus plotu gali būti paskaičiuotas pagal tokią formulę:

Šioje formulėje N žymi plokštelių skaičių, S0 – atstumą tarp dviejų plokštelių statmeniems plokštelių paviršiams kryptimi, H – grotelių aukštį. S0 ir N gali būti paskaičiuoti pagal atitinkamai
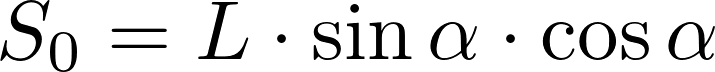
ir
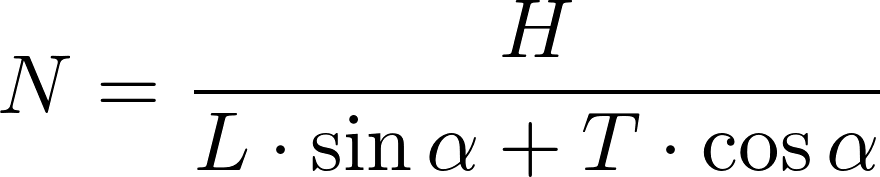
formules. Šiose formulėse L žymi plokštelės plotį, T – plokštelės storį, α – plokštelių pasukimo kampą. Išsprendus plokštelių skaičiaus N lygtį α atžvilgiu, gauname
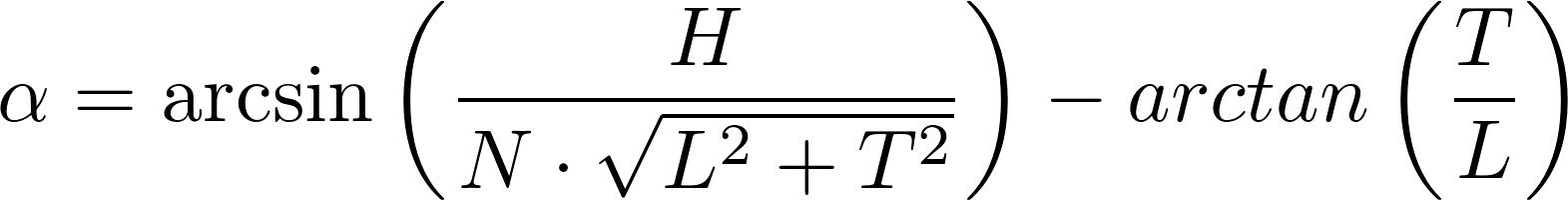
Paskutinioji formulė yra skaičiuoklės pagrindas. Jos pagalba galima paskaičiuoti pasukimo kampą visiems galimiems plokštelių skaičiams. Žinant pasukimo kampą galima paskaičiuoti atstumą tarp plokštelių S0, o iš jo ir oro srauto santykį S.
