Anuitetas

Internete galima rasti nemažai anuitetinės paskolos skaičiuoklių, kuriose įvedus paskolos sumą, metinę palūkanų normą ir paskolos suteikimo trukmę, galima sužinoti išsamius duomenis apie paskolą: periodinio mokėjimo sumą, paskolos likutį po kiekvieno mokėjimo, kokia mokėjimo dalis skirta palūkanų mokėjimui, o kuri dalis skolos dengimui, kiek bus sumokėta palūkanų ir t.t. Tačiau informacijos, kaip skaičiuojami paskolos duomenys, nėra daug. Šiame įraše yra pateikiama anuitetinės paskolos duomenų skaičiavimo formulės ir jų naudojimo pavyzdys.

Žiūrint iš besiskolinančiojo pusės, anuitetinis paskolos mokėjimo būdas yra gana paprastas, nes periodinio mokėjimo už paskolą suma yra fiksuoto dydžio visą paskolos išsimokėjimo laikotarpį. Tačiau paskaičiuoti tokio mokėjimo būdo periodinius mokėjimus ir kitus duomenis yra sudėtingiau nei, pavyzdžiui, linijinio mokėjimo būdo duomenis.

Svarbiausias paskolos duomuo – periodinio mokėjimo suma. Šios sumos formulę galima išvesti iš lygties, kurios sąlyga yra tokia: visų periodinių mokėjimų skolos dengimo dalies suma turi būti lygi visai paskolos sumai. Kadangi palūkanos skaičiuojamos nuo likusios sumokėti paskolos dalies, o periodinio mokėjimo suma lygi paskolos padengimo ir palūkanų dalių sudėčiai, minėtą sąlygą galima užrašyti taip:

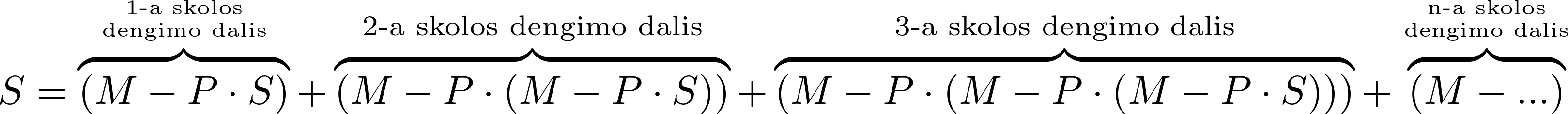
S = \overbrace{\left( M - P \cdot S\right)}^{\text{1-a skolos}\atop\text{dengimo dalis}} + \overbrace{\left(M - P \cdot \left( M - P \cdot S \right)\right)}^\text{2-a skolos dengimo dalis} + \overbrace{\left(M - P \cdot \left( M - P \cdot \left( M - P \cdot S \right)\right)\right)}^\text{3-a skolos dengimo dalis} + \overbrace{\left(M - ...\right)}^{\text{n-a skolos}\atop\text{dengimo dalis}}

kurioje S yra paskolos suma, P – mokėjimo periodo palūkanų norma, M – periodinio mokėjimo suma, N – mokėjimų skaičius, t.y. paskolos terminas.

Sudauginus lygties narius ir pritaikius binomo formulę, lygtį galima suprastinti:

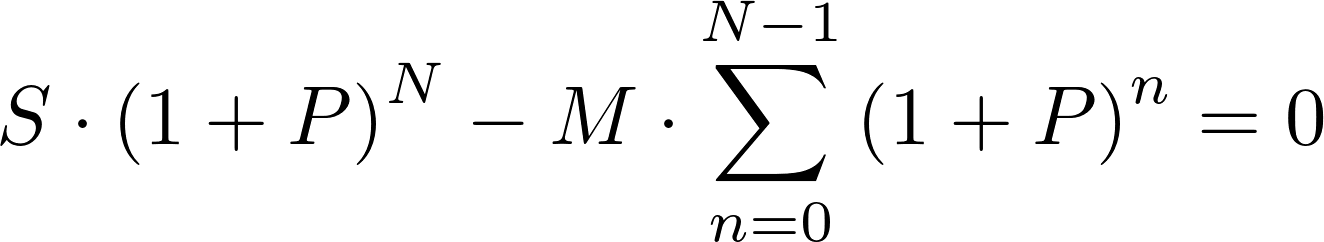
S \cdot \left( 1 + P \right)^N - M \cdot \sum_{n=0}^{N-1} \left( 1 + P \right)^n = 0

Pritaikius geometrinės progresijos sumos formulę, lygtį galima dar labiau suprastinti:

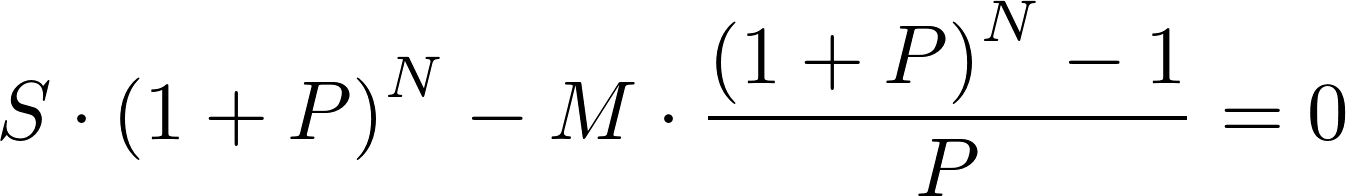
S \cdot \left( 1 + P \right)^N - M \cdot \frac{\left( 1 + P \right)^N - 1}{P} = 0

Iš paskutinės lygties gaunama galutinė anuitetinės paskolos periodinio mokėjimo sumos skaičiavimo formulė:

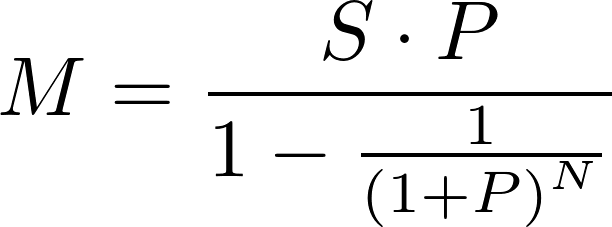
M = \frac{S \cdot P}{1 - \frac{1}{\left( 1 + P \right)^N}}

Žinant periodinio mokėjimo sumą, galima paskaičiuoti kitus paskolos duomenis.

Kiek iš viso bus sumokėta palūkanų, t.y. paskolos kainą, galima paskaičiuoti pagal tokią formulę:

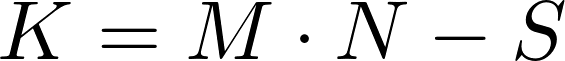
Šiek tiek sudėtingiau yra paskaičiuoti paskolos likutį po kiekvieno periodinio mokėjimo ir kiekvieno periodinio mokėjimo sumos paskolos padengimo bei palūkanų dalis. Taip yra dėl to, kad kiekvieną duomenį reikia atvaizduoti suapvalintą mažiausio galimo piniginio vieneto, t.y. cento, tikslumu. Dėl šios priežastis net negalima užrašyti universalių formulių, pagal kurias būtų galima paskaičiuoti šių duomenų vertes, nes skaičiavimo būdų gali būti keletas. Žemiau pateikiamas vienas iš būdų.

Pirmiausia paskaičiuojama periodinio mokėjimo sumos palūkanų dalis. Ji paskaičiuojama pagal tokią formulę:

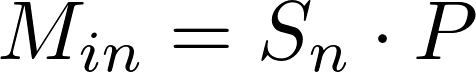
kur S_n yra paskolos likutis prieš n-tą mokėjimą.

Žinant mokėjimo sumos palūkanų dalį, mokėjimo sumos paskolos padengimo dalį galima paskaičiuoti pagal tokią formulę:

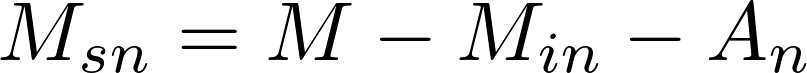
kur A_n yra ankstesnio mokėjimo sumos paskolos padengimo dalies apvalinimo likutis. Šis likutis savo ruožtu paskaičiuojamas pagal tokią formulę:

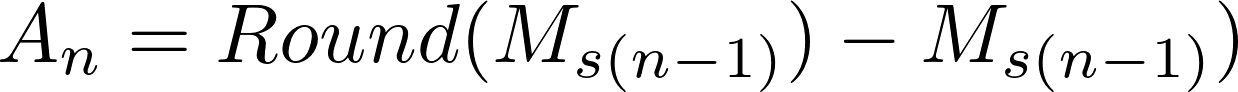
kur Round yra funkcija, apvalinanti reikšmę cento tikslumu. Pirmo mokėjimo atveju apvalinimo likutis yra lygus nuliui, t.y. A₁=0.

Pakolos likutis prieš n-tą mokėjimą paskaičiuojamas pagal tokią formulę:

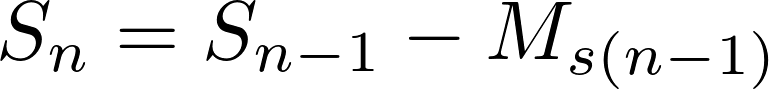
Pirmo mokėjimo atveju paskolos likutis yra lygus paskolos sumai, t.y. S₁=S.

Skaičiuojant paskolos duomenis pagal aukščiau pateiktas formules, visos gautos paskolos duomenų vertės turi būti atvaizduojamos suapvalintos cento tikslumu.

Pavyzdžiui, jei paskolos suma yra 300 €, metinė palūkanų norma – 6 %, paskolos terminas – 12 mėn. ir sutarta, kad periodinis mokėjimas už paskolą bus atliekamas kas mėnesį, mėnesinė įmoka paskaičiuojama taip:

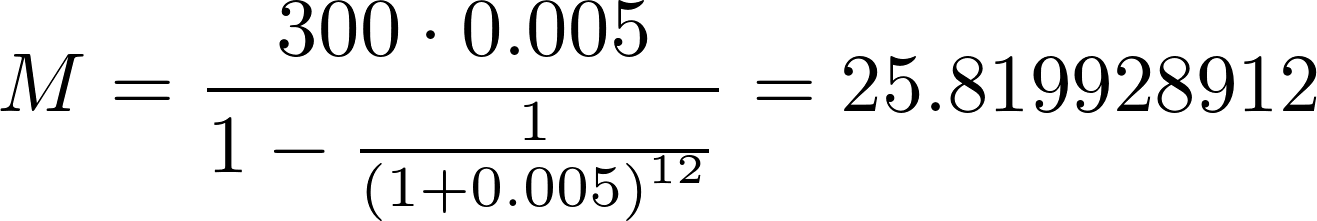
M = \frac{300 \cdot 0.005}{1 - \frac{1}{\left( 1 + 0.005 \right)^{12}}} = 25.819928912

Kadangi pavyzdyje mokėjimo periodas yra mėnuo, skaičiuojant mokėjimo sumą buvo naudojama 0,5 % mėnesinė palūkanų norma, kuri gaunama metinę palūkanų normą 6 % padalinus iš 12, t.y. mėnesių skaičiaus metuose.

Žemiau esančioje lentelėje pateikiamas paskolos mokėjimo grafikas, kurio duomenys paskaičiuoti naudojant aukščiau pateiktas formules.

Mėnuo n	Paskolos likutis S_n	Mokėjimo suma M	Paskolos dalis M_sn	Palūkanų dalis M_in
1	300,00	25,82	24,32	1,50
2	275,68	25,82	24,44	1,38
3	251,24	25,82	24,57	1,25
4	226,67	25,82	24,68	1,14
5	201,99	25,82	24,81	1,01
6	177,18	25,82	24,94	0,88
7	152,24	25,82	25,05	0,77
8	127,19	25,82	25,19	0,63
9	102,00	25,82	25,31	0,51
10	76,69	25,82	25,43	0,39
11	51,26	25,82	25,57	0,25
12	25,69	25,82	25,69	0,13

GitHub projekto annuity-calculator svetainėje yra patalpinta programėlė, kurios pagalba galima paskaičiuoti paskolos mokėjimo grafiką. Programėlėje naudojamos šiame įraše aprašytos formulės.

Žyma: Anuitetas

Anuitetinės paskolos duomenų skaičiavimo formulės